slacr_

Just to record my life and thoughts.
笔记/编程/杂乱/极简

126Archives20Categories

[计组笔记]数据的机器层次表示

Apr 20, 2023CS5025 words in 34 min

计算机组成原理笔记

数值的表示

有符号数和无符号数

有符号数有符号位， 无符号数无， 全部二进制位都是数值位.
真值 不同表示法所代表的真正意义的值， 比如 1011（原码）, 1100(反码), 1101(补码)他们的真值都是-3
机器数 数值在计算机内的二进制表示

原码表示法

最高位符号位, 其余数值位
原码中0有两种不同的表示 [+0]_{原} 0000 和 [-0]_{原} 1000

纯小数

原码形式为: X_s\quad . \quad X_1\quad X_2\quad \cdots \quad X_n

\begin{equation} \left[ X \right]_{原} = \left\{ \begin{aligned} & X & \qquad 0 \leq X \lt 1 \\ & 1 - X = 1 + \lvert X \rvert & \qquad -1 \lt X \leq 0 \end{aligned} \right . \nonumber \end{equation}

例:
真值 0.01 原码 0.01
真值 -0.01 原码 1-(-0.01) = 1 + 0.01 = 1.01

纯整数

原码形式为 X_s\quad X_1\quad X_2\quad \cdots \quad X_n

\begin{equation} \left[ X \right]_{原} = \left\{ \begin{aligned} & X & \qquad 0 \leq X \lt 2^n \\ & 2^n - X = 2^n + \lvert X \rvert & \qquad -2^n \lt X \leq 0 \end{aligned} \right . \nonumber \end{equation}

例:
真值3, 机器数字长4, 那么符号位0 , 数值位011, 原码即 0 011
真值-3, 机器数字长4, 那么符号位1, 数值位 2^3 - (-3) = 2^3 + 3 = 11 , 原码即 1 011

规律

正数不变
负数符号位置1

反码表示法

原码的符号位不能直接参与运算, 因此引入了反码.
正数不变; 负数符号位不变, 数值位取反
反码中0也有两种不同的表示 [+0]_{反} 0000 和 [-0]_{反} 1111
也正是因为0的两种不同表示, 导致反码如果在计算过程中入过越过0 则会产生差错, 因为0这个真值在一个循环中占了两位, 比如-1反码 1110, 加2以后变成 0000, 对应原码 0000 ,真值0 , 产生一位的偏错.

纯小数

原码形式为: X_s\quad . \quad X_1\quad X_2\quad \cdots \quad X_n

\begin{equation} \left[ X \right]_{反} = \left\{ \begin{aligned} & X \quad(mod 2) & \qquad 0 \leq X \lt 1 \\ & (2 - 2^{-n}) + X \quad(mod 2) & \qquad -1 \lt X \leq 0 \\ \end{aligned} \right . \end{equation}

例:
真值0.375, 机器码字长4, 反码值为0.375, 反码为 0.011
真值-0.375, 原码1.011, 机器码字长4, 反码值为 (2-2^{-3}) + (-0.375) = 1.5 , 反码 1.100
也可以用二进制运算 10_{2} - 0.001_2 - 0.011_2 = 1.100_2
二进制计算只能计算无符号数, 负数改成减法.

纯整数

原码形式为 X_s\quad X_1\quad X_2\quad \cdots \quad X_n

\begin{equation} \left[ X \right]_{补} = \left\{ \begin{aligned} & X \quad(mod 2^{n+1} - 1) & \qquad 0 \leq X \lt 2^n \\ & (2^{n+1} - 1) + X \quad(mod 2^{n+1} - 1) & \qquad -2^n \lt X \leq 0 \\ \end{aligned} \right . \end{equation}

例:
真值6, 机器码字长4, 反码值6, 反码0110
真值-6, 原码1110, 机器码字长4, 反码值 2^{3+1} - 1 + (-6) = 9 , 反码 1001

规律
正数不变
负数符号位不变, 数值位取反

补码表示法

为了解决反码计算中0的两种表示会出错的问题, 引入补码.
补码中真值0的表示唯一, [+0]_{补} = [-0]_{补} = 0000
补码在数值上可以用原码取反加一来计算
但补码用模和同余的概念更好理解. 计算机只完成正数的加法运算, 计算减法转换为负数加法, 负数转换成计算具有相同效力的正数(补码), 不论什么进制, 补码都可以直接用公式计算出来. 这种思想相当巧妙.
1000_{补} 既没有原码也没有反码, 通常用来表示最小值

模和同余

模 Module, 计量器的容量, 比如4位二进制计数器计数状态 0000 ~ 1111, M = 2^4 = 16

同余
两个整数A 和B 除以同一个正整数M ,所得余数相同
A和B在以M为模时相等(AB同余), 可以记作,

A = B \qquad (mod M)

M = 2, 所有奇数都是同余的, 余数为1

取模运算与取余运算
常见的整数除法求余数, 比如计算 -10 / 3
先当浮点数计算 -10 / 3 = -3.333
取模运算 向 -\infty 取整, 得到模为-4, 余数 -10 - (-4 * 3) = 2
取余运算 向 0 取整, 得到商为-3, 余数 -10 - (-3 * 3) = -1

取模和取余对于同号数来说运算结果都是相同的, 因为正数无论是向0还是负无穷取整结果都一样.

列:

利用模和同余将减法转换为加法

例如钟表, 由一组循环的10进制数 1~12 组成
将钟表逆时针拨2小时, 和顺时针拨10小时结果都一样, 因为-2与10同余 -2 = 10 (mod 12),
不同的只是模值, -2取模是-1, 10取模是0.

可见, 只要确定模值, 就可以将负数转换为正数, 这样计算机只用完成无符号的加法操作, 加上一个负数等同于加上与这个负数同余的正数.

对于任意数X

\begin{equation} \left[ X \right]_{补} = \left\{ \begin{aligned} & X \quad(mod M) & \qquad 0 \leq X \lt \frac{M}{2} \\ & M + X \quad(mod M) & \qquad -\frac{M}{2} \leq X \lt 0 \\ \end{aligned} \right . \end{equation}

这样就可以将区间 [-\frac{M}{2}, \frac{M}{2}) 转换到正数区间 [ 0, M) 上的运算

计算机中的补码表示

纯小数
原码形式为: X_s\quad . \quad X_1\quad X_2\quad \cdots \quad X_n

\begin{equation} \left[ X \right]_{补} = \left\{ \begin{aligned} & X \quad(mod 2) & \qquad 0 \leq X \lt 1 \\ & 2 + X = 2 - |X| \quad(mod 2) & \qquad -1 \leq X \lt 0 \\ \end{aligned} \right . \end{equation}

例:
真值0.375 , 机器数字长4, 补码值为0.375, 机器码形式为 0.011
真值-0.375, 机器数字长4, 补码值为2 + (-0.375) = 2 - 0.375 = 1.625, 即 1.101
或者运算的时候直接用二进制
10_2 - 0.011_2 = 1.101_2

纯整数
原码形式为 X_s\quad X_1\quad X_2\quad \cdots \quad X_n

\begin{equation} \left[ X \right]_{补} = \left\{ \begin{aligned} & X \quad(mod 2^{n+1}) & \qquad 0 \leq X \lt 2^n \\ & 2^{n+1} + X = 2^{n+1} - |X| \quad(mod 2^{n+1}) & \qquad -2^n \leq X \lt 0 \\ \end{aligned} \right . \end{equation}

例:
真值5 , 机器数字长4, 补码值为5, 机器码形式为 0101
真值-5, 机器数字长4, 真值范围 -2^3 ~ 2^3-1 , 模为 2^4 , 补码值为 2^{4} + (-5) = 11, 机器码为 1011

真值与三种机器数对照

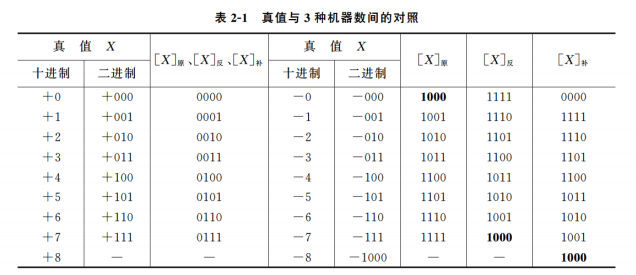
机器数的定点表示与浮点表示

现代计算机大都小数浮点表示, 整数定点表示

定点表示法

小数点位置固定不变.

定点小数

纯小数, 小数点位置固定在最高有效数值位之前, 符号位之后. 小数点约定位置不占位.

不难算出:
补码表示的情况下:
X_{max+} = 1 - 2^{-n}
X_{min+} = 2^{-n}
X_{max-} = -2^{-n}
X_{min-} = - 1
范围 -1 ~ 1-2^{-n}

定点整数

纯整数, 小数位隐含固定在最低有效数值位之后

范围 -2^{n} ~ 2^{n}-1

浮点表示法

形式与范围

形如:

N = M \times r^{E}

M (Mantissa) 尾数
r 底数, 通常为2
E (Exponent)阶码, 或叫指数

阶码和尾数都是带符号的定点数, 尾数为纯小数, 常用原码或补码表示；阶码为纯整数，常用移码或补码表示。
浮点数的表示范围主要由阶码的位数来决定，有效数字的精度主要由尾数的位数来决定

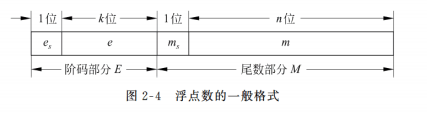
这里尾数和阶码均用补码表示.
不难算出:
X_{max+} = (1-2^{-n}) \times 2^{2^{k}-1}
X_{min+} = 2^{-n} \times 2^{-2^{k}}
X_{max-} = -2^{-n} \times 2^{-2^{k}}
X_{min-} = -2^{2^{k}-1}

规格化浮点数

充分利用尾数的有效位, 要求尾数的最高数位必须是一个有效值.
要求

\frac{1}{r} \leq |M| \lt 1

通过调整阶码使得数值位最高位的真值必定为1

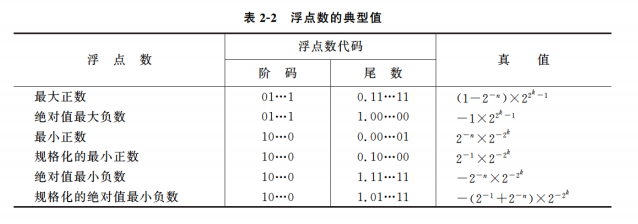
当运算结果大于最大正数时称为正上溢，小于绝对值最大负数时称为负上溢，正上溢和负上溢统一称为上溢，数据一旦产生上溢，计算机必须中止运算操作，进行溢出处理。
当运算结果在0至规格化最小正数之间称为正下溢，在0至规格化的绝对值最小负数之间称为负下溢，正下溢和负下溢统一称为下溢，数据一旦出现下溢，计算机一般不做任何处理，仅仅置成机器零即可。
只要浮点数的尾数为0,不论阶码为何值，一般也当作机器零处理。为了保证浮点数0表示形式的唯一性，规定了机器零的标准格式，即：尾数为0,阶码为最小值(绝对值最大的负数)。

阶码的移码表示法

[X]_{移} = 偏置值 + X

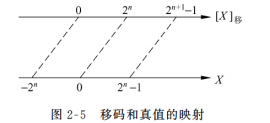
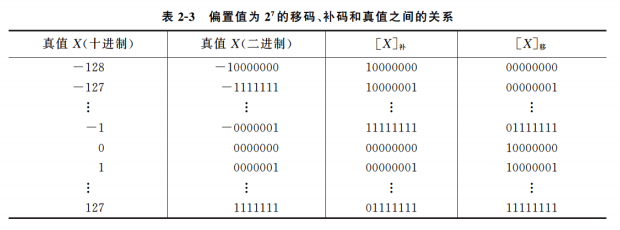
浮点数尾数的基数

r的大小影响浮点数表示范围与精度.
在以 r 进制为尾数基数的浮点数中，当尾数的位数为二进制 n 位时，就相当于r 进制的尾数有n’个数位，其中 \lceil n'=n/log_{2}r \rceil

IEEE 754 标准浮点数

在目前常用的80x86系列微型计算机中，通常设有支持浮点运算的部件。在这些机器中的浮点数采用 IEEE754 标准，它与前面介绍的浮点数格式有一些差别。

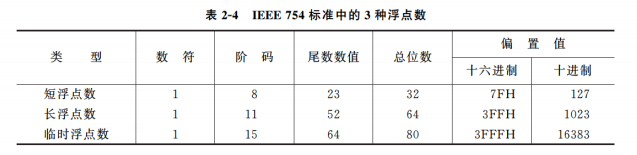
短浮点数又称为单精度浮点数，长浮点数又称为双精度浮点数，它们都采用隐含尾数最高数位的方法，这样无形中又增加了一位尾数. 临时浮点数又称为扩展精度浮点数，它没有隐含位。

通常，将 IEEE 754 短浮点数规格化的数值 v 表示为:

v = (-1)^{S} \times (1.f) \times 2^{E-127}

S 代表符号位，S=0表示正数，S=1 表示负数；E 为用移码表示的阶码；f 是尾数的小数部分.
为了表示 \infty 和一些特殊的数值，E 的最小值0和最大值255将留作他用。
最小移码 E=1,最移码 E=254,所以短浮点数的阶码真值的取值范围为-126～127。
当 E 和 M 均为全0时，表示机器零；当 E 为全1,m 为全0时，表示 \pm \infty .

非数值的表示

ASCII字符编码

ASCII (American Standard Code for Information Interchange), 使用7位二进制表示一个字符, 计算机中一般使用一个字节来存放一个字符, 最左边一位可以作为奇偶校验位，用来检查错误，也可以用于西文字符和汉字的区分标识, 首位为0标志为西文字符.

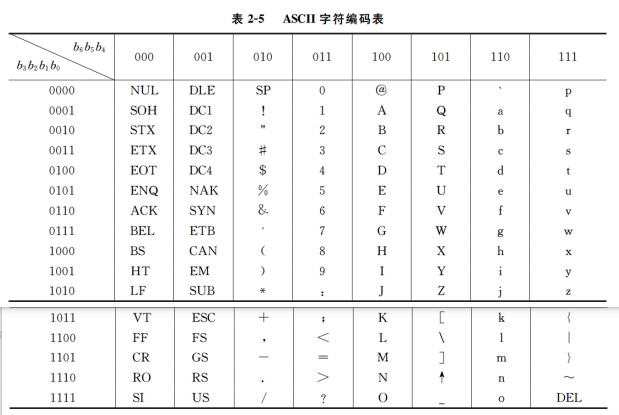
字符串的存放

向量法 一片物理相邻且逻辑相邻的连续空间, 数组
串表法 放在储存空间任意位置, 逻辑相邻, 链表.方便删改, 空间效率低

汉字的表示

汉字区位码

区位码将汉字编码 GB 2312—80 中的6763个汉字分为94个区，每个区中包含94个汉字(位),区和位组成一个二维数组，每个汉字在数组中对应一个唯一的区位码。汉字的区位码定长4位，前两位表示区号，后两位表示位号，区号和位号用十进制数表示，区号从01到94,位号也从01到94。例如，“中”字在54区的48位上，其区位码为“54—48”.
第1～15区包含西文字母、数字和图形符号，以及用户自行定义的专用符号(统称非汉字图形字符);第16～55区为一级汉字；第56～87区为二级汉字；87区以上为空白区，可供造新字用.
区位码的与国标码的关系

国标码=区位码(十六进制)+2020H

为什么加 2020H
GB 2312(国标码)对于英文字符进行了重新编码, 但对于ASCII中前32个控制字符继续沿用. 所以保留前32个字符. 加上2020H的偏移量.

汉字国标码

GB-2312-80
汉字国标码, 信息交换用汉字编码字符集基本集, 创建于1980年, 有6763个常用汉字. 每个汉字使用两个字节, GB2312将代码表分为94个区，对应第一字节；每个区94个位，对应第二字节. 两个字节的值分别为区号值和位号值加32（20H）.
每个字节只使用低7位编码, 多能表示出128×128=16384个汉字。

汉字机内码

汉字可以通过不同的输入码输入，但在计算机内部其内码是唯一的。因为汉字处理系统要保证中西文的兼容，当系统中同时存在 ASCII 码和汉字国标码时，将会产生二义性。
汉字机内码也是两字节长的代码，它是在相应国标码的每个字节最高位上加1所得.

汉字机内码=汉字国标码+8080H

GBK
汉字内码扩展规范, “国标”、“扩展”汉语拼音的第一个字母.是在GB2312-80标准基础上的内码扩展规范. 共23940个码位，共收录了21003个汉字，完全兼容GB2312-80标准.
采用单双字节变长编码，英文使用单字节编码，完全兼容ASCII字符编码，中文部分采用双字节编码。

汉字字形码

汉字字形码是指确定一个汉字字形点阵的代码，又称汉字字模码或汉字输出码。在一个汉字点阵中，凡笔画所到之处，记为1,否则记为0。
汉字输出时经常使用，所以要把各个汉字的字形信息固定存储起来，存放各个汉字字形信息的实体称为汉字库。

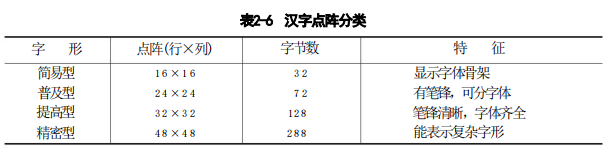
Unicode

统一代码(Unicode)又称万国码、单一码，它是由多语言软件制造商组成的统一码联盟制定的可以容纳世界上所有文字和符号的字符编码方案。

编码方式

Unicode 的编码方式与国际标准 ISO/IEC 10646 的通用字符集(Universal CharacterSet,UCS)概念相对应，两者的码表兼容，并共同调整任何未来的扩展。
Unicode 的基本方法是用一个16位的二进制数(2字节)来表示 Unicode 中的每个符号，这意味着允许表示65536个不同的字符或符号。这种符号集被称为基本多语言平面(BMP),基本多语言平面的字符编码为 U+hhhh,其中每个 h 代表一个十六进制数字.

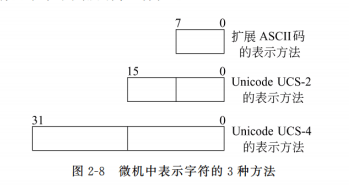
字符 A 用 UCS-2 表示为“U+0041”,而其对应的 UCS-4 的后两个字节与UCS-2一致，前两个字节则所有位均为0。

实现方式

Unicode 的实现方式不同于编码方式。一个字符的 Unicode 编码是确定的，但是在实际传输过程中，由于不同系统平台的设计不一定一致，以及出于节省空间的考虑，Unicode编码的实现方式会有所不同。 Unicode 的实现方式称为 Unicode 转换格式 (UnicodeTranslation Format,UTF),目前存在的 UTF 格式有 UTF-7、UTF-7.5、UTF-8 UTF-16 和UTF-32。

UTF-32 四个字节表示一个字符

UTF-16 2字节储存，但无法兼容于ASCII编码。

UTF-8 采取可变长编码方案, 分成单字节、双字节、三字节、四字节模式. 汉字字符占三个字节.

不同编码方案编码解码造成乱码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
package myPack;

import java.io.UnsupportedEncodingException;
import java.util.Arrays;

public class testForCharset {
    public static void main(String[] args) {
        String data = "a我b";
        byte[] data_bytes = data.getBytes();   // 按照默认编码方式转换成二进制码, 这里是UTF-8
        System.out.println(Arrays.toString(data_bytes)); // 调用Arrays类中的toString方法将数组转换成字符串, UTF-8 汉字占三个字节, 开头是0, 所以是负数
        byte[] data_bytes_GBK;
        try {
            data_bytes_GBK = data.getBytes("GBK");  // alt enter 将错误抛出, 使用GBK编码
        } catch (UnsupportedEncodingException e) {
            throw new RuntimeException(e);
        }
        System.out.println(Arrays.toString(data_bytes_GBK));   // 按照GBK编码, 汉字占两个字节
        String s_default = new String(data_bytes);        // 使用string构造器按默认编码解码
        System.out.println(s_default);
        String s_GBKencode_UTFdecode = new String(data_bytes_GBK);
        System.out.println(s_GBKencode_UTFdecode);      // GBK编码, UTF-8解码会出现问题, 汉字占两个字节, UTF-8中没有编码一位汉字要三个字节, 且有特定格式要求, 这里只能别解码成未知的乱码
        String s_GBK = null; // 构造器指定参数, GBK格式解码
        try {
            s_GBK = new String(data_bytes_GBK, "GBK");
        } catch (UnsupportedEncodingException e) {
            throw new RuntimeException(e);
        }
        System.out.println(s_GBK);

    }
}

数据校验码

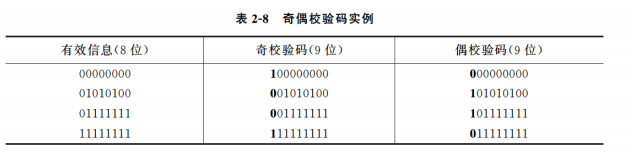
奇偶校验码

校验位更具信息位1的个数来初始化与用来检验.

Hamming codes

一种多重奇偶校验, 其实现原理是：在有效信息位中加入几个校验位形成汉明码，使码距比较均匀地拉大，并把汉明码的每一个二进制位分配到几个奇偶校验组中。当某一位出错后，就会引起有关的几个校验位的值发生变化，这不但可以发现错误，还能指出错误的位置，为自动纠错提供了依据。
码距: 两个合法代码对应位上编码不同的位数称为码距，又称海明距离。
校验位的位数K 和信息位的位数N 应该满足不等式

CRC

循环冗余校验码(Cyclic Redundancy Check,CRC), 通过除法运算来建立有效信息位和校验位之间的约定关系
若信息位为 N 位，校验位为 K 位，则该校验码被称为(N+K,N)码。

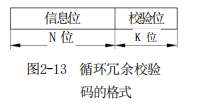
编码步骤:

  1. 把待编码的 N 位有效信息表示为多项式M(X)

  2. 把 M(X)左 移 K 位，得到 M(X)×X^K 这样空出了K位，以便拼装 K 位余数。

  3. 选取一个K+1 位的产生多项式 G(X),对 M(X)×X^K 做模2除。

    \frac{M(X) × X^K }{G(X)} = Q(X) + \frac{R(X)}{G(X)}

  4. 把左移 K 位以后的有效信息与余数R(X)做模2加减，拼接为CRC码，此时的CRC码共有 N+K 位

    M(X) × X^{K} + R(X)=Q(X) × G(X)

例:

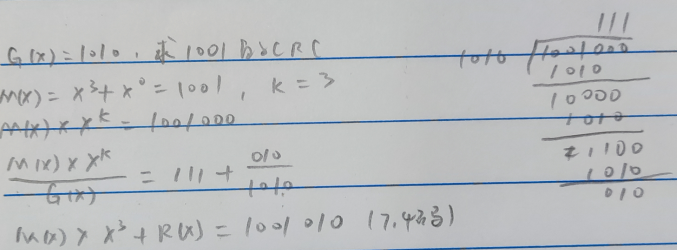
把接收到的 CRC码用约定的生成多项式 G(X)去除，如果正确，则余数为0;如果某一位出错，则余数不为0。不同的位数出错其余数不同，余数和出错位序号之间有唯一的对应关系。

生成多项式的选择

  • 任何一位发生错误都应使余数不为0。
  • 不同位发生错误应当使余数不同。
  • 对余数做模2除法，应使余数循环。

参考

  1. 《计算机组成原理（第四版）》 IBSN 9787302530213 蒋本珊编著
  2. 百度百科-GBK
  3. GB2312区位码转机内码为什么要同时加上2020H和8080H？
  • Author:

    slacr_

  • Copyright:

  • Published:

    April 20, 2023

  • Updated:

    April 20, 2023

Buy me a cup of coffee ☕.

支
read 1000000
1 数值的表示
1.1 有符号数和无符号数
1.2 原码表示法
1.2.1 纯小数
1.2.2 纯整数
1.3 规律
1.4 反码表示法
1.4.1 纯小数
1.4.2 纯整数
1.5 补码表示法
1.5.1 模和同余
1.5.2 利用模和同余将减法转换为加法
1.5.3 计算机中的补码表示
1.6 真值与三种机器数对照
2 机器数的定点表示与浮点表示
2.1 定点表示法
2.1.1 定点小数
2.1.2 定点整数
2.2 浮点表示法
2.2.1 形式与范围
2.2.2 规格化浮点数
2.2.3 阶码的移码表示法
2.2.4 浮点数尾数的基数
2.2.5 IEEE 754 标准浮点数
3 非数值的表示
3.1 ASCII字符编码
3.2 字符串的存放
3.3 汉字的表示
3.3.1 汉字区位码
3.3.2 汉字国标码
3.3.3 汉字机内码
3.3.4 汉字字形码
3.4 Unicode
3.4.1 编码方式
3.4.2 实现方式
3.5 数据校验码
3.6 奇偶校验码
3.7 Hamming codes
3.8 CRC