[C++笔记]群体类和群体数据的组织一

群体类和群体数据

基本数据类型是 c++ 编译系统预定义的，而自定义类型的数据是由多个基本类型或自定义类型的元素组成，称之为群体数据。
对于群体数据，仅有系统预定义的操作是不够的，在很多情况下，还需要设计与某些具体问题相关的特殊操作，并按照面向对象的方法将数据与操作封装起来，这就是群体类。
群体可分为两种:线性群体和非线性群体。线性群体中的元素按位置排到有序, 如数组。非线性群体不用位置顺序来标识元素，如拓扑图.

函数模板和类模板

模板是 C++ 支持参数化程序设计的工具，通过它可以实现参数化多态性。所谓参数化多态性，就是将程序所处理的对象的类型参数化，使得一段程序可以用于处理多种不同类型的对象。

类模板的多文件结构中必须声明与实现都在头文件中. 因为如果分文件编写, 在编译的时候类模板没有实例化就不会产生目标代码. 当其他源文件引用该模板头文件时, 虽然能实例化各个类模板的声明, 但无法将函数的实现实例化, 因为编译器对每个源文件的编译时分别进行的. 编译时无法相互访问. 得不到模板的具体实现, 连接时就会发生错误.
如果将函数模板、类模板的成员函数和类模板的静态数据成员的定义都放在头文件中，就可以避免这一问题，因为这些定义在编译任何一个源文件时都是可见的，编译器可以按需对它们进行实例化。

由于函数模板和类模板的成员函数一般放在头文件中，这与内联函数相似，因此容易被人误以为函数模板和类模板的成员函数都会被自动当作内联函数处理。其实函数模板和类模板的成员函数既可以是内联函数，也可以是非内联函数，将其声明为内联函数的方法与非模板的函数一样，都要使用 inline 关键字，或将成员函数写在类定义内。

函数模板

(1)函数模板本身在编译时不会生成任何目标代码，只有由模板生成的实例会生成目标代码。
(2) 被多个源文件引用的函数模板，应当连同函数体一同放在头文件中，而不能像普通函数那样只将声明放在头文件中。
(3) 函数指针也只能指向模板的实例，而不能指向模板本身。

#include <iostream>
using namespace std;

template<typename T>		// 或者 class 关键字
void showT(T t) {
	cout << typeid(t).name() << endl;
}

int main() {
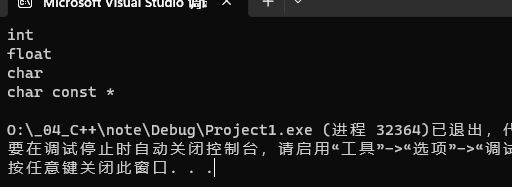
	showT<int>(3);
	showT<float>(4.0);
	showT<char>('A');
	showT<>("test");	// 也可以不写模板参数, 编译器自动识别, 最好还是写上
	return 0;
}

类模板

使用类模板使用户可以为类定义一种模式，使得类中的某些数据成员、某些成员函数的参数、返回值或局部变量能取任意类型(包括系统预定义的和用户自定义的)。
类是对一组对象的公共性质的抽象，而类模板则是对不同类的公共性质的抽象，因此类模板是属于更高层次的抽象。由于类模板需要一种或多种类型参数，所以类模板也常常称为参数化类。

#include <iostream>
using namespace std;

class Intel_CPU {};
class AMD_CPU {};
class NVIDIA_GPU {};
class AMD_GPU {};

template <class C, class G>
class Computer {
public:
	Computer() {}
	Computer(C c, G g) : c(c), g(g) {}
	void getInfo();
private:
	C c;
	G g;
};

template <class C, class G>
void Computer<C, G>::getInfo() {
	cout << typeid(c).name() << " " << typeid(g).name() << endl;
}
// 类外实现模板类的成员函数, 有点复杂


int main() {
	Intel_CPU IC;
	AMD_CPU AC;
	Computer<Intel_CPU, AMD_GPU> c_1(IC, AMD_GPU());
	Computer<AMD_CPU, NVIDIA_GPU> c_2(AC, NVIDIA_GPU());
	// 这里不知道为什么全部该成创建匿名对象不行, 创建一个就可以, 可能是生存期的问题
	c_1.getInfo();
	c_2.getInfo();
	return 0;
}

线性群体

线性群体中的元素次序与其位置关系是对应的。在线性群体中，又可按照访问元素的不同方法分为直接访问、顺序访问和索引访问。
两种特殊的线性群体栈和队列。

直接访问群体一一数组类

实现一个简单的动态数组类模板 Array 。它由任意多个位置连续的、类型相同的元素组成，其元素个数可在程序运行时改变。它虽然比 vector 简单，但与 vector 的工作原理没有本质差别。

C++ 中，如果想将自定义类型T的对象隐含或显式地转换为S类型，可以将operator S定义为T的成员函数。这样，在把T类型对象显式隐含转换为S类型，或用static_cast 显式转换为S类型时，该成员函数会被调用。转换操作符的重载函数不用指定返回值的类型，这是由于这种情况下重载函数的返回类型与操作符名称一致，因此c++ 标准规定不能为这类函数指定返回值类型(也不要写 void)
而当对象本身为常数时，为了避免通过指针对数组内容进行修改，只能将对象转换为常指针。

实现动态数组类模板

#ifndef ARRAY_H
#define ARRAY_H
#include <cassert>

template<class T>
class Array {
private:
	T* list;	// 指针, 用于动态分配内存
	int size;	// 数组大小
public:
	Array(int sz = 50);				// 构造函数
	Array(const Array<T>& arr);		// 复制构造函数
	~Array();
	Array<T>& operator= (const Array<T>& rhs);		// 重载 = 
	T& operator[] (int i);							// 重载 []
	const T& operator[] (int i) const;				// 针对const重载 []
	operator T* ();									// 重载到 T* 类型的转换
	operator const T* () const;
	int getSize() const;							// 获得数组大小
	void resize(int sz);							// 修改数组大小
};


// 构造函数
template<class T>
Array<T>::Array(int sz) {
	assert(sz >= 0);								// sz 初始化应 >= 0 
	size = sz;
	list = new T[size];
}

// 析构函数
template <class T>
Array<T>::~Array() {
	delete[] list;
}

// 复制构造函数
template <class T>
Array<T>::Array(const Array<T>& a) {
	size = a.size;									// 复制大小
	list = new T[size];								// 申请内存
	for (int i = 0; i < size; i++) {				// 复制每个元素
		list[i] = a.list[i];							
	}
}

// 重载 = 运算符, 实现对象间的赋值
template<class T>
Array<T>& Array<T>::operator= (const Array<T>& rhs) {
	if (&rhs != this) {			// 避免 a = a 这种情况
		if (size != rhs.size) {	 
		// 如果数组大小与rhs不同, 不好改变已分配大小,选择删除原有内存, 重新分配
			delete[] list;				
			size = rhs.size;
			list = new T[size];
		}
		for (int i = 0; i < size; i++) {			// 复制每个元素
			list[i] = rhs.list[i];				
		}
	}
	return *this;				// 返回当前对象的引用
}
// 返回一个引用, 不仅是为了链式编程, C++中'='运算允许做左值, (a = b) = c + 1, 如果返回对象则不可做左值, 并且调用复制构造额外开销, 一般返回引用 

// 重载下标运算符 []
template<class T>
T& Array<T>::operator[](int n) {
	assert(n >= 0 && n < size);  // 数组下标控制
	return list[n];
}
//返回值应为一个引用, 因为返回值将要作为左值, arr[i] = xx, 如果是返回对象则是不可做左值的.

template<class T>
const T& Array<T>::operator[](int n) const {
	assert(n >= 0 && n < size);			// 同上, 重载const修饰条件下的数组下标运算[]
	return list[n];
}

// 重载指针运算符, 将Array类的对象名转换为T类型指针, 指向当前对象的私有数组
// 为了发生隐式转换编译器能自动调用, 例如函数接受一个int* 指针, 但传入的是 Array<int>* p 的指针
// 这时编译器会尝试转换 (int*)p, 调用重载的 类型转换运算符 
template<class T>
Array<T>::operator T* () {
	return list;
}

template<class T>
Array<T>::operator const T*() const {
	return list;
}

// 获取数组大小
template<class T>
int Array<T>::getSize() const {
	return size;
}


// 修改数组大小
template<class T>
void Array<T>::resize(int sz) {
	assert(sz >= 0);
	if (sz == size) return;
	T* newList = new T[sz];			// 创建新数组并分配空间
	int n = (sz < size) ? sz : size; // 填入数据的长度应该为 较小的数组长度 n
	for (int i = 0; i < size; i++) {
		newList[i] = list[i];		// 将前n个元素复制到新数组
	}
	delete[] list;			// 删除旧数组
	list = newList;			// 指向新数组
	size = sz;				// 更新size 
}

# endif  // ARRAY_H

测试

#include <iostream>
using namespace std;
#include "Array.h"

int main() {
	Array<float> Arr_f(20);
	for (int i = 0; i < Arr_f.getSize(); i++) {
		Arr_f[i] = (float)i;
	}
	for (int i = 0; i < Arr_f.getSize(); i++) {
		cout << fixed << Arr_f[i] << " ";
	}
	cout << endl;
	// defaultfloat 默认浮点数格式化是不显示精度尾0, 可以改成fixed 显示精度 
	
	Arr_f.resize(100);
	cout << Arr_f.getSize() << endl;
	cout << Arr_f[20] << endl;   // 未初始化
//	cout << Arr_f[200] << endl;   // debug 触发断言
	const float* f = (const float*)Arr_f;  // 转换为常指针
	cout << f[0] << endl;

	float* ff = const_cast<float*>(f);	
	cout << ff[0] << endl;
	return 0;
 }

顺序访问群体一一链表类

链表是一种动态数据结构，可以用来表示顺序访问的线性群体。

实现链表类模板

节点类模板

结点类的数据成员中应该包括数据域和指针域的内容，函数成员中应该含有对数据和指针进行初始化的方法(函数) ，以及在本结点之后插入新结点和删除后继结点的方法。

#pragma once
#include "Node.h"


// 定义类模板
template<class T>
class LinkedList {
private:
	Node<T>* front, * rear;		// 表头和表尾指针
	Node<T>* prevPtr, * currPtr; // 记录当前遍历位置的指针, 用于插入删除操作更新
	int size;					// 表中元素个数
	int position;				// 当前元素在表中的位置序号, 函数reset 使用

	Node<T>* newNode(const T& item, Node<T>* ptrNext = NULL);	// 生成新结点
	void freeNode(Node<T>* p);				// 释放结点
	void copy(const LinkedList<T>& L);		// 将链表L复制到当前表, 被复制构造函数和operator'=' 调用

public:
	LinkedList();			// 构造函数
	LinkedList(const LinkedList<T>& L);  // 复制构造函数
	~LinkedList();				// 析构函数
	LinkedList<T>& operator=(const LinkedList<T>& L);  // 重载复值运算符 = 
	
	int getSize() const;				// 返回链表元素个数
	bool isEmpty() const;				// 返回链表是否为空

	void reset(int pos = 0);			// 初始化游标的位置
	void next();						// 使游标移动到下一结点
	bool endOfList() const;				// 游标是否到链尾
	int currentPostion(void) const;		// 返回游标当前位置

	void insertFront(const T& item);	// 表头插入结点
	void insertRear(const T& item);		// 表尾插入结点
	void insertAt(const T& item);		// 当前结点之前插入结点
	void insertAfter(const T& item);	// 当前结点之后插入结点

	T deleteFront();					// 删除头结点
	void deleteCurrent();				// 删除当前节点

	T& data();							// 返回当前节点对应数据的引用
	const T& data() const;				// 返回常引用
	
	void clear();						// 清空链表, 释放内存, 被析构和operator=调用
};

// 函数实现

// 生成新结点
template<class T>
Node<T>* LinkedList<T>::newNode(const T& item, Node<T>* ptrNext /* = NULL */) {
	Node<T>* p_node = new Node<T>(item, ptrNext);
	size++;
	return p_node;
}

// 释放结点
template<class T>
void LinkedList<T>::freeNode(Node<T>* p) {
	delete p;
	size--;
}

// 复制链表
template<class T>
void LinkedList<T>::copy(const LinkedList& L) {
	if (isEmpty(L)) return;				// 如果链表空返回
	LinkedList newList;
	L.reset(1);							// 从第二个结点开始
	for (int i = 1; i < L.getSize(); i++) {
		insertAfter(L.data());
		L.next();
	}
}


// 构造函数
template<class T>
LinkedList<T>::LinkedList() {
	size = 0;
	position = 0;
	Node<T>* p_node = newNode(0, NULL);						// 初始化头结点
	front = rear = prevPtr = currPtr = p_node;
}

// 复制构造
template<class T>
LinkedList<T>::LinkedList(const LinkedList<T>& L) {
	copy(L);
}

// 析构
template<class T>
LinkedList<T>::~LinkedList() {
	clear();
}

// 重载 = 
template<class T>
LinkedList<T>& LinkedList<T>::operator=(const LinkedList<T>& L) {
	copy(L);
	clear(L);
}

// 返回链表元素个数
template<class T>
int LinkedList<T>::getSize() const {
	return size ;				
}

// 返回链表是否为空
template<class T>
bool LinkedList<T>::isEmpty() const {
	if (front == rear) return true;
	return false;
}

// 初始化游标的位置
template<class T>
void LinkedList<T>::reset(int pos /* =  0 */) {
	if (pos == 0) return;					// 
	currPtr = prevPtr = front;					// 从头开始偏移
	position = pos;								// 偏移完成 position 应等于 pos
	for (int i = 0; i < position; i++) {		// prevPtr 和 currPtr移动到对应位置
		next();
	}
}

// 游标移动到下一结点
template<class T>
void LinkedList<T>::next() {
	prevPtr = currPtr;
	currPtr = currPtr->nextNode();
	position++;
}

// 游标是否到链尾
template<class T>
bool LinkedList<T>::endOfList() const {
	if (position == size) return true;			
	return false;
}

// 返回游标当前位置
template<class T>
int LinkedList<T>::currentPostion() const {
	return position;
}

// 表头插入结点
template<class T>
void LinkedList<T>::insertFront(const T& item) {
	Node* p_node = newNode(item, front);
	front = p_node;

}

// 表尾插入结点
template<class T>
void LinkedList<T>::insertRear(const T& item){
	Node* p_node = newNode(item, NULL);
	rear->insertAfter(p_node);
	rear = p_node;
}

// 当前节点之前插入结点
template<class T>
void LinkedList<T>::insertAt(const T& item) {
	Node<T>* p_node = newNode(item, currPtr);
	prevPtr->insertAfter(p_node);
	currPtr = p_node;					// currPtr前移
	position--;
}

// 当前结点之后插入结点
template<class T>
void LinkedList<T>::insertAfter(const T& item) {
	Node<T>* p_node = newNode(item, currPtr->nextNode());
	currPtr->insertAfter(p_node);
	currPtr = p_node;						// currPtr后移
	position++;
}

// 删除头结点
template<class T>
T LinkedList<T>::deleteFront() {
	Node<T>* temp = front;
	T data = front->data;
	front = front->nextNode();
	freeNode(temp);
	return data;
}

// 删除当前结点
template<class T>
void LinkedList<T>::deleteCurrent() {
	prevPtr->insertAfter(currPtr->nextNode());
	Node<T>* temp_curr = currPtr;
	currPtr = currPtr->nextNode();
	freeNode(temp_curr);
}

// 返回当前结点对应数据的引用
template<class T>
T& LinkedList<T>::data(){
	return currPtr->data;
}

// 返回常引用
template<class T>
const T& LinkedList<T>::data() const {
	return currPtr->data;
}

// 清空链表
template<class T>
void LinkedList<T>::clear() {
	while (front != rear) {
		Node<T>* temp = front->nextNode();
		freeNode(front);
		front = temp;
	}
	freeNode(front);
}

测试

#include "LinkedList.h"
#include <iostream>
using namespace std;

int main() {
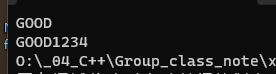
	LinkedList<char> L;
	L.insertAfter('G');			// 后插
	L.insertAfter('O');			
	L.insertAfter('O');
	L.insertAfter('D');
	L.reset(1);
	for (int i = 0; i < 4; i++) {
		cout << L.data();
		L.next();
	}
	cout << endl;
	L.insertAt('4');			// 前插
	L.insertAt('3');
	L.insertAt('2');
	L.insertAt('1');
	L.reset(1);
	for (int i = 0; i < 8; i++) {
		cout << L.data();
		L.next();
	}
	return 0;
}

感觉实现有点问题, position 还没用. 书上给的是游标来控制插入删除取数的位置, 既有头插也有尾插, 用双向链表的节点好实现些.

栈类

栈的基本状态有:一般状态、栈空、栈满。当栈中没有元素时称为栈空;当栈中元素个数达到上限时，称为栈满;栈中有元素、但未达到栈满状态时，即处于一般状态。如果用静态数组存储存元素，则元素个数达到数组声明的元素个数时即为栈满。如果使用动态数组或链表，则可以根据需要设置或不设置元素的最大个数。

无论采用哪种数据结构，栈类中都应该包括下列基本操作:初始化、入栈、出栈、栈清空、访问栈顶元素、检测栈的状态(满或空)。

实现栈类模板

#pragma once
#include <cassert>
// 定义类模板
template<class T, int SIZE = 50>
class Stack {
private:
	T list[SIZE];			
	int top;				// 栈顶位置
public:
	Stack();
	void push(const T& item);	// 入栈
	T pop();					// 出栈
	void clear();				// 清空栈
	const T& peek() const;	// 访问栈顶元素
	bool isEmpty() const;	// 栈是否空
	bool isFull() const;	// 栈是否满
};

// 模板实现
template<class T, int SIZE> 
Stack<T, SIZE>::Stack() : top(-1) {}		// 构造函数, 初始化栈顶为-1

// 入栈
template<class T, int SIZE>
void Stack<T, SIZE>::push(const T& item) {
	assert(!isFull());				// 栈满报错
	list[++top] = item;				// 新元素压入栈顶
}

// 出栈
template<class T, int SIZE> 
T Stack<T, SIZE>::pop() {
	assert(!isEmpty());				// 栈空报错
	return list[top--];				// 栈顶出栈
}

// 访问栈顶元素
template<class T, int SIZE>
const T& Stack<T, SIZE>::peek() const {
	assert(!isEmpty());				// 栈空报错
	return list[top];				// 返回栈顶元素
}

// 栈是否空
template<class T, int SIZE>
bool Stack<T, SIZE>::isEmpty() const {
	return top == -1;
}

// 栈是否满
template<class T, int SIZE>
bool Stack<T, SIZE>::isFull() const {
	return top == SIZE - 1;
}

// 清空栈
template<class T, int SIZE>
void Stack<T, SIZE>::clear() {
	top = -1;
}

测试

#include <iostream>
using namespace std;
#include "Stack.h"

int main() {
	Stack<char, 50> s;
	s.push('L');
	s.push('I');
	s.push('V');
	s.push('E');
	while (!s.isEmpty()) {
		cout << s.peek();
		s.pop();
	}
	return 0;
	// EVIL
}

队列类

队列也有三种基本状态:一般状态、队空、队满。当队中没有元素时称为队空;当队中元素个数达到上限时，称为队满;队中有元素，但未达到队满状态时，即处于一般状态。
如果用静态数组存储队列元素，则元素个数达到数组声明的元素个数时即为队满。如果使用动态数组或链表，则可以根据需要设置或不设置元素的最大个数。

无论采用哪种数据结构，队列类的数据成员都应包括:队列元素、队头指针和队尾指针。队列类中函数成员应该能够实现下列基本操作:初始化、入队、出队、清空队列、访问队首元素、检测队列的状态(满、空、队列长度)。

如果用静态数组存储队列元素，每当有元素出队时，队中元素都要向队头方向移动。因此数据移动量大，效率不高。

可以将队列设计为循环队列。也就是在想象中将数组弯曲成环形，元素出队时，后继元素不移动，每当队尾达到数组最后一个元素时，便再回到数组开头。为了使队尾达到数组最后一个元素时，再回到数组开头，需要运用取余运算(%)。另外，为了判断队列的状态，需要对元素个数进行记录。当元素个数为0时，队空。当元素个数等于最大值时，队满。

实现

#ifndef  QUEUE_H
#define QUEUE_H
#include <cassert>

// 类模板定义
template<class T, int SIZE = 50>
class Queue {
private:
	int front, rear, count;			// 队头指针 对位指针 元素个数
	T list[SIZE];					// 元素数据
public:
	Queue();			// 构造函数
	void insert(const T& item);		// 入队
	T remove();						// 出队
	void clear();					// 清空队列
	const T& getFront() const;		// 访问队首元素

	int getLength() const;		// 返回队列元素个数
	bool isEmpty() const;		// 是否队空
	bool isFull() const;		// 是否队满

};

// 类实现

// 构造函数
template<class T, int SIZE>
Queue<T, SIZE>::Queue() : front(0), rear(0), count(0) {}

// 入队
template<class T, int SIZE>
void Queue<T, SIZE>::insert(const T& item) {
	assert(count != SIZE);				// 队满报错
	count++;
	list[rear] = item;					// 插入队尾
	rear = (rear + 1) % SIZE;			// 队尾后移, 取余实现循环, 余数范围在 [0, SIZE-1] 循环
}

// 出队
template<class T, int SIZE>
T Queue<T, SIZE>::remove() {
	assert(count != 0);					// 队空报错
	count--;
	int temp = front;					// 记录队首
	front = (front + 1) % SIZE;		    // 队头后移, 取余实现循环
	return list[temp];					// 返回首元素的值
}

// 访问队列首元素
template<class T, int SIZE>
const T& Queue<T, SIZE>::getFront() const {
	return list[front];
}

// 返回元素个数
template<class T, int SIZE>
int  Queue<T, SIZE>::getLength() const {
	return count;
}

// 是否队空
template<class T, int SIZE>
bool Queue<T, SIZE>::isEmpty() const {
	return count == 0;
}


// 是否队满
template<class T, int SIZE>
bool Queue<T, SIZE>::isFull() const {
	return count == SIZE;
}

// 清空队列
template<class T, int SIZE>
void Queue<T, SIZE>::clear() {
	count = front = rear = 0;
}

#endif // ! QUEUE_H

测试

#include<iostream>
using namespace std;
#include "Queue.h"

int main() {
	Queue<int, 10> q;
	for (int i = 0; !q.isFull() ; i++) {
		q.insert(i);
	}
	for (int i = 0; !q.isEmpty(); i++) {
		cout << q.getFront();
		q.remove();
	}
	// 0123456789
	return 0;
}

参考

《C++语言程序设计（第4版）》 IBSN 9787302227984
C++参考手册
Microsoft C++文档

Author:
slacr_
Copyright:
Published:
April 29, 2023
Updated:
April 29, 2023

Buy me a cup of coffee ☕.

支