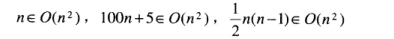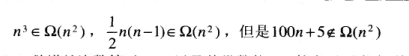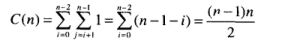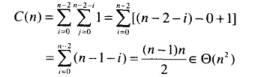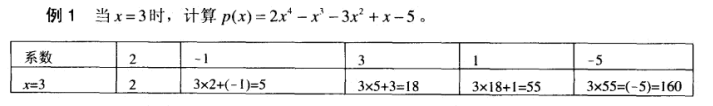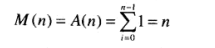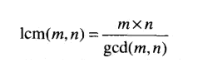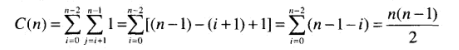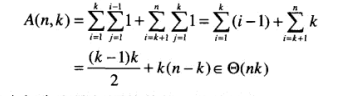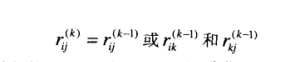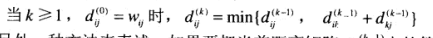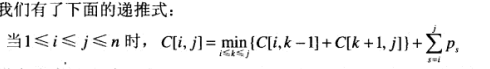slacr_

Just to record my life and thoughts.
笔记/编程/杂乱/极简

126Archives20Categories

[算法设计与分析基础]复习

Jun 19, 2023Algo7115 words in 47 min

万恶的考试周, 大学就是考试了才开始学. 应试就是多记几个题型和知识点, 决胜2天.

绪论&算法效率分析

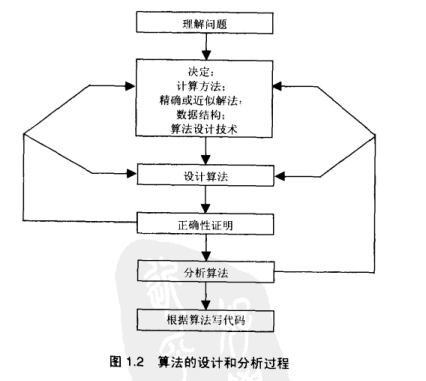
算法概念

一系列指令的集合, 这些指令所构成的逻辑能在利用有限的计算资源(时间空间复杂度)完成某种或某类计算. 算法就是解决问题的步骤与方法, 是严格符合推理逻辑的.

算法的特性

  • 输入输出, 有穷性和确定性
  • 正确性: 对于任意合法输入, 经过有限时间的计算能得到输出.
  • 效率:
    • 时间效率: 反应运行速度
    • 空间效率: 反应运行时间
  • 简单性: 相对容易理解和实现
  • 一般性: 所解决问题的一般性和所接受输入的一般性, 建立更通用的算法.
  • 最优性

重要的问题类型

  • 排序
  • 查找
  • 字符串处理
  • 图问题
  • 组合问题
  • 几何问题
  • 数值问题

欧几里得算法求最大公约数GCD(Greatest Common Divisor)

gcd(m,n)=gcd(n,m mod n)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include<iostream>
using namespace std;

inline int GCD(int a, int b) {
	int r;
	while (b) {
		r = a % b; 
		a = b;
		b = r;
	}
	return a;
}

// 递归写法
inline int nest_GCD(int a, int b) {
	if (!b) return a;
	int r = a % b;
	return nest_GCD(b, r);
}

int main() {
	cout << GCD(54, 36) << endl;
	// a	b	r
	// 54	36	undef
	// 36	18	18
	// 18	0	0
	cout << nest_GCD(108, 162) << endl;
	return 0;
}

基本数据结构

  • 线性数据结构
    • 线性列表
      • 数组
      • 链表
        • 单链表
        • 双链表
      • 队列
        • 优先队列
      • 栈
  • 图
    • 表示 G<V, E>, V- vertex, 顶点集合, E -edge, 边集合, 每个元素是一对定点, 称为边.
    • 顶点对(u, v)相互邻接, 通过无向边(u, v)相连接, u v 称为端点, u 和 v 和该边相关联
    • 完全图: 各顶点都和其他顶点相连, K_|v|
    • 稠密图和稀疏图: 相对于完全图缺的边数量较少为稠密, 反之稀疏.
    • 图的表示法
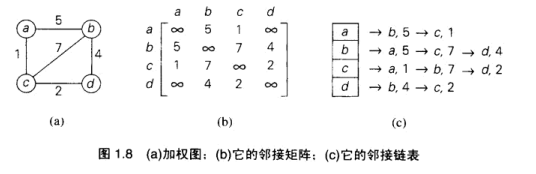
      • 邻接矩阵
        • n*n的布尔矩阵, 每个值表示第i个顶点到第j个顶点是否有边连接.
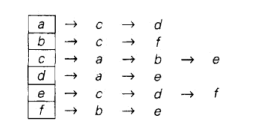
      • 邻接链表
        • 每一个顶点用一个邻接链表表示, 表头为每个顶点, 每个链表其余的为和这个顶点相邻接的所有顶点. 对于一个给定的顶点, 它的邻接链表指出了对应邻接矩阵中值为1的列.
    • 加权图
      • 给边赋了值的图
        对应的邻接矩阵称权重矩阵或成本矩阵, 不存在相邻边, 权重取 infinite
    • 路径, 环, 连通分量, 联通度
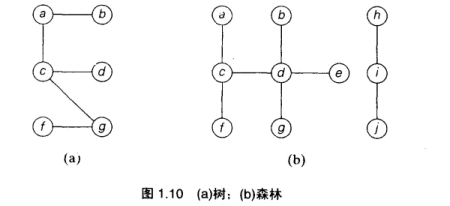
  • 树(自由树)
    • 连通无回路的图, 无回路不一定连通的图称为森林, 它的每个连通分量是一棵树.
    • 树的边数比定点数少1, |E| = |V| - 1
    • 有根树
      • 任选一个顶点, 作为根.
    • 树的深度: 顶点v的深度为根到v的简单路径的长度.
    • 树的高度: 根到叶子结点最常的简单路径长度.
    • 有序树
      • 每个顶点的子女皆是有序的.
      • 二叉查找树
      • 多路查找树
  • 集合与字典
    • 互不相同项的无序组合.
    • 集合的表示方法
      • 第一种, 表示通用集合的大集合U的子集, U中元素个数n, 可以采取位向量的表示法, 用一个长度为n的位串, 子集中存在U中该位元素就置1.
      • 第二种, 用线性列表表示, 不过列表式有序且可包含重复元素的, 可以用多重集或包的概念, 绕过唯一性要求.
    • 字典: 能实现对集合或多重集查找, 增加, 删除一个元素操作的数据结构称为字典.
  • 抽象数据类型(ADT), 定义数据项的抽象对象集合和对集合中对象的操作.描述数据结构和对应操作的一个概念.

算法效率分析

输入规模: 将算法效率表示为一个以输入规模 n 为参数的函数.
基本操作: 最重要的操作, 对时间贡献最大, 元运算.
算法程序的运行时间估算:
MATHJAX-SSR-11
T(n)为总运行时间, C_{op} 为一次基本操作执行时间, C(n)为基本操作执行次数, n为输入规模.

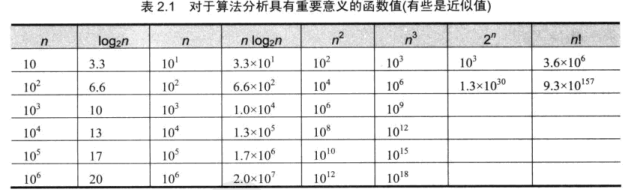
增长次数:
随输入规模n的增大, C(n)为不同函数类型会很大程度决定效率, 一个指数级操作次数的算法随输入规模n的执行次数增长非常快, 有限计算资源下只能计算较小的输入规模.

算法最优 最差 平均效率

字面意思, 最优效率即输入规模为n时, 算法在最好的情况下(执行次数最少)的效率. 平局效率的评估较为复杂, 必须做出一定假设.
比如顺序查找算法, 最优执行次数1, 一次就找到; 最差n, 无此元素; 平均需要考虑待查元素在此集合中的概率p, 该元素在每一位的概率1/n, 平均次数: (1-p)*n + p(1/n + 2/n + … + n/n)

渐进符号

O(g(n))为算法的增长次数小于等于g(n)及其常数倍的集合, 增长次数上界.

Ω(g(n))同理, 增长次数小于等于g(n)及其常数倍. 增长次数的下界. 如果一个算法的效率类型属于Ω(g(n)), 那么这个算法的增长次数一定是比g(n)高阶或者等阶的.

θ(g(n)) 增长次数同阶, 等于g(n)常数倍, 反应增长次数的的效率类型与g(n)一样.

更一般的用极限来比较:

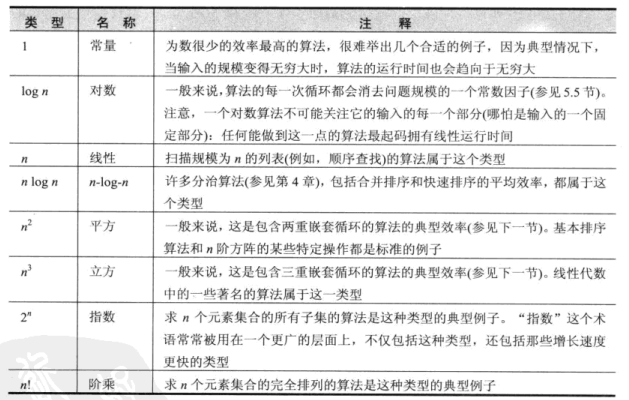
比值为0或常量说明, t(n)属于O(g(n)); 为常量 说明t(n)属于θ(g(n)); 为无穷或常量说明t(n)属于Ω(g(n)).

基本渐进效率类型

非递归算法效率分析一般步骤

  1. 确定输入规模, 通常选 n
  2. 确定基本操作, 通常循环最内层
  3. 检查基本操作的执行次数是否只依赖输入规模, 因为如果不是, 执行次数就还受到其他条件影响, 需要引入其他参数确定执行次数. 分别讨论最优, 最差, 平均.
  4. 建立算法基本操作执行次数的求和表达式.
  5. 计算得到增长次数, 分析效率类型.

递归算法分析

  1. 同非递归一二三
  2. 建立递推关系, 给出相应的初始条件(递归退出条件)
  3. 计算递归表达式, 得到增长次数, 确定效率类型.

Fibonacci数列

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<iostream>
using namespace std;
#include<vector>

int Fibonacci(int n) {
	if (n <= 1) return n;
	return Fibonacci(n - 1) + Fibonacci(n - 2);
}

// 减少重复调用计算相同值， 空间换时间
int better_Fibonacci(int n) {
	vector<int> nums;
	nums.resize(n);
	nums[0] = 0;
	nums[1] = 1;
	for (int i = 2; i < n; i++) {
		nums[i] = nums[i - 1] + nums[i - 2];
	}
	return nums[n-1];
}


int main() {
	int n = 10;
	for (int i = 0; i < 10; i++) {
		cout << Fibonacci(i) << " ";
	}
	cout << endl;

	cout << better_Fibonacci(10) << endl;
	return 0;
}

递归效率
M(n) = M(n-1) + M(n-2)+1
M(n) = 2^{n-3} +n+2 , 2{^n} 效率类型

蛮力法

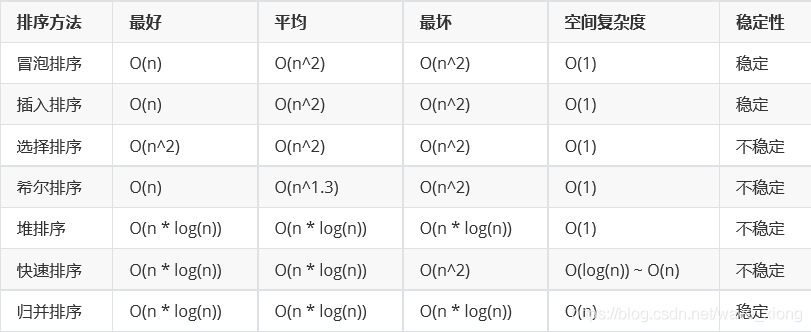
选择排序和冒泡排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include<iostream>
using namespace std;
#include<bits/stdc++.h>

template<class T>
void printVector(vector<T>& nums) {
	for (auto i : nums) cout << i << " ";
	cout << endl;
}

template<class T>
void selection_sort(vector<T>& nums) {
	for (int i = 0; i < nums.size()-1; i++) {
		int min_idx = i;
		for (int j = i+1; j < nums.size(); j++) {
			if (nums[j] < nums[min_idx]) {
				min_idx = j;
			}
		}
		swap(nums[i], nums[min_idx]);
		printVector(nums);
	}
}

template<class T>
void bubble_sort(vector<T>& nums) {
	for (int i = 0; i < nums.size()-1; i++) {   // n -1 趟
		for (int j = 0; j < nums.size()-i-1; j++) {  // 每一趟进行比较和交换, 将最大值放到最后
			if (nums[j] > nums[j + 1]) swap(nums[j], nums[j + 1]);
		}
		printVector(nums);
	}
}

int main() {
	vector<int> nums = { 89,45,68,90,29,34,17 };
	selection_sort(nums);
	nums = { 89,45,68,90,29,34,17 };
	cout << "=========================" << endl;
	bubble_sort(nums);
	return 0;
}

  • 选择排序没有最优最差平均之分, 因为每次查找最小值都要遍历之后所有元素, 执行次数

    效率类型 属于 O(n^2)

  • 最优顺序不交换, 最差倒序次次交换, 基本操作都是比较, 效率类型 O(n^2)

顺序查找和蛮力字符串匹配

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include<iostream>
using namespace std;
#include<bits/stdc++.h>

template<class T> 
int sequential_search(vector<T>& nums, T key) {
	for (int i = 0; i < nums.size(); i++) {
		if (nums[i] == key) {
			return i;
		}
	}
	return -1;
}

int brute_force_search(string s, string p) {
	int m = p.length();
	int n = s.length();
	for (int i = 0; i <= n - m; i++) {
		int j;
		for (j = 0; j < m; j++) {
			if (s[i + j] != p[j]) {
				break;
			}
		}
		if (j == m) {
			return i;
		}
	}
	return -1;
}

int main() {
	vector<int> v = { 1, 2, 3, 4 ,5 };
	cout << sequential_search(v, 3) << endl;
	cout << brute_force_search("djkasfoiadfahj", "kas");
	return 0;
}

最近对问题和凸包问题暴力算法

最近对问题: 计算每两个点之间的距离, 取最小

凸包问题:
先要明白凸集合: 一个平面点集, 对于该集合中任意两点之间的线段都属于该集合.

凸包问题就是要再一个点集中求解构造该凸包的集合.
暴力解法为利用数学方法给每两个点建立一条直线, 然后判断其余点是否在其同一侧.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include<iostream>
using namespace std;
#include<bits/stdc++.h>
int get_dist2(pair<pair<int, int>, pair<int, int>> pair_dots) {
	return pow(pair_dots.first.first - pair_dots.second.first, 2) + pow(pair_dots.first.second - pair_dots.second.second, 2);
}

string print_dot(pair<int, int> dot) {
	return string("(").append(to_string(dot.first)).append( ",").append(to_string(dot.second)).append( ")");
}

void nearest_dot_pair(vector<pair<int, int>>& dots) {
	// 最近对, 蛮力法
	pair<pair<int, int>, pair<int, int>> pair_dots = {dots[0], dots[1]};
	double min_dist = get_dist2(pair_dots);
	for (int i = 0; i < dots.size(); i++) {
		for (int j = i+1; j < dots.size(); j++) {
			int curr_dist = get_dist2(make_pair(dots[i], dots[j]));
			if (min_dist > curr_dist) {
				min_dist = curr_dist;
				pair_dots = { dots[i], dots[j] };
			} 
		}
	}
	cout << "最近点对: " << print_dot(pair_dots.first) << " " << print_dot(pair_dots.second) << endl;
	cout << "最短距离^2: " << min_dist << endl;
}

typedef  pair<int, int> dot;
typedef  pair<pair<int, int>, pair<int, int>> line;
typedef vector<pair<int, int>> dots;

int at_which_side(line l, dot d) {
	if (l.first.first == l.second.first) return d.first - l.first.first;
	else if (l.first.second == l.second.second) return d.second - l.first.second;
	else {
		// 两点式
		int x1 = l.first.first;
		int y1 = l.first.second;
		int x2 = l.second.first;
		int y2 = l.second.second;
		int x = d.first;
		int y = d.second;
		return ((y2 - y1*1.0) / (x2 - x1)) * (x - x1) - y + y1;
	}
}

void calc_convexhull(dots& ds) {
	// 凸包问题, 蛮力法
	set<dot> s;
	int i, j, k;
	for (i = 0; i < ds.size()-1; i++) {
		for (j = i + 1; j < ds.size(); j++) {
			int cnt1 = 0;
			int cnt2 = 0;
			int cnt3 = 0;
			for (k = 0; k < ds.size(); k++) {
				if (at_which_side(line(ds[i], ds[j]), ds[k]) > 0) {
					cnt1++;
				}
				else if (at_which_side(line(ds[i], ds[j]), ds[k]) == 0) {
					cnt2++;
				} else {
					cnt3++;
				}
			}
			if (!cnt3 || !cnt1) { s.insert(ds[i]); s.insert(ds[j]); };
		}
	}
	cout << "边界点:" << endl;
	for (dot d : s) {
		cout << print_dot(d) << " ";
	}
}



int main() {
	vector<pair<int, int>> dots = { make_pair(3, 4), make_pair(0,0), make_pair(10, 0),  make_pair(0, 10), make_pair(10, 10), make_pair(5, 5)};
	nearest_dot_pair(dots);
	cout << "==============================" << endl;
	calc_convexhull(dots);
	return 0;
}

穷举查找

列举所有情况得到满足条件的组合

  • 旅行商问题
  • 背包问题
  • 分配问题

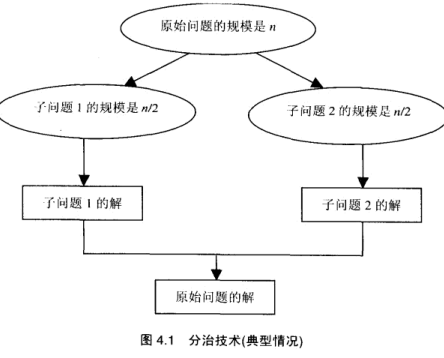
分治法

将问题的实例划分为同一个问题的较小实例.

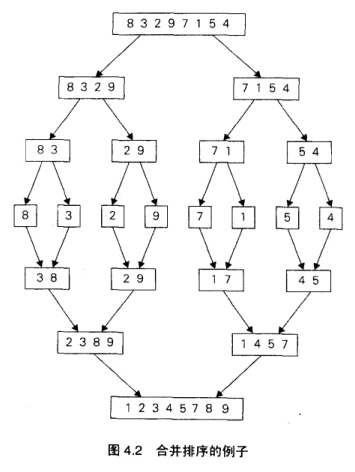
合并排序 快速排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<iostream>
using namespace std;
#include<bits/stdc++.h>

// 合并排序
template<class T>
void merge(vector<T>& nums, int start, int mid, int end) {
    vector<T> temp(end-start+1);
    int i = start, j = mid+1, k = 0;
    while (i <= mid && j <= end) {
        if (nums[i] <= nums[j]) {
            temp[k++] = nums[i++];
        } else {
            temp[k++] = nums[j++];
        }
    }
    while (i <= mid) {
        temp[k++] = nums[i++];
    }
    while (j <= end) {
        temp[k++] = nums[j++];
    }
    for (int p = 0; p < k; p++) {
        nums[start+p] = temp[p];
    }
}

template<class T>
void merge_sort(vector<T>& nums, int start, int end) {
    if (start >= end) {
        return;
    }
    int mid = start + (end - start) / 2;
    merge_sort(nums, start, mid);
    merge_sort(nums, mid+1, end);
    merge(nums, start, mid, end);
}

template<class T>
void printVector(vector<T>& nums) {
    for (auto i : nums) cout << i << " ";
    cout << endl;
}

int main() {
    vector<int> nums = {3, 5, 1, 6, 2, 7, 4, 8};
    merge_sort(nums, 0, nums.size()-1);
    printVector(nums);
    return 0;
}

核心思想是通过不断比较确定分隔符使左右区间整体有序, 缩小区间范围往下递归.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
#include <iostream>
#include <vector>

using namespace std;

template<class T>
int partition(vector<T>& nums, int start, int end) {
    T pivot = nums[end];
    int i = start;
    for (int j = start; j < end; j++) {
        if (nums[j] < pivot) {
            swap(nums[i], nums[j]);
            i++;
        }
    }
    swap(nums[i], nums[end]);
    return i;
}

template<class T>
void quick_sort(vector<T>& nums, int start, int end) {
    if (start >= end) {
        return;
    }
    int pivot = partition(nums, start, end);
    quick_sort(nums, start, pivot-1);
    quick_sort(nums, pivot+1, end);
}

template<class T>
void printVector(vector<T>& nums) {
    for (auto i : nums) cout << i << " ";
    cout << endl;
}

int main() {
    vector<int> nums = {3, 5, 1, 6, 2, 7, 4, 8};
    quick_sort(nums, 0, nums.size()-1);
    printVector(nums);
    return 0;
}

效率类型都是 nlogn

二叉树遍历

前序中序后序

大整数乘法和Srassen矩阵乘法

分治法解最近对和凸包问题

…

减治法

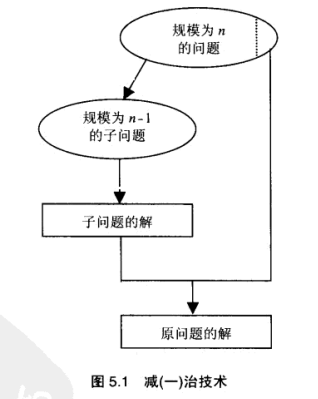
减治技术利用了一个问题给定实例的解和同样问题较小实例的解之间的某种关系。一旦建立了这种关系，我们既可以从顶至下(递归地),也可以从底至上(非递归地)地来运用该关系。减治法有3种主要的变种：

  • 减去一个常量
  • 减去一个常量因子
  • 减去的规模是可变的

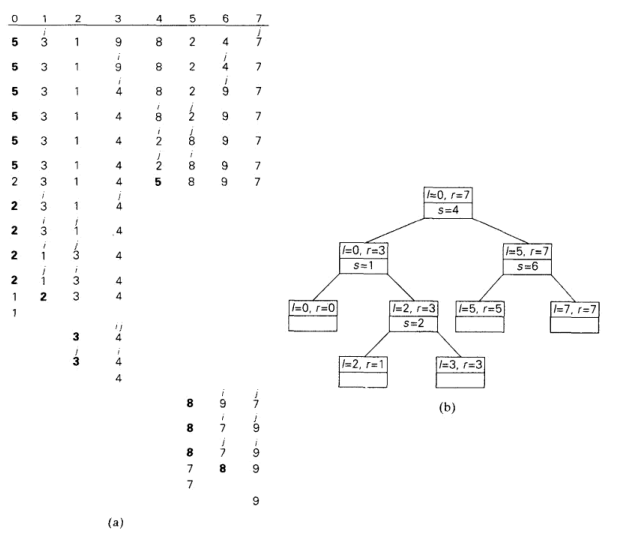
插入排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
#include <iostream>
using namespace std;
#include <bits/stdc++.h>

template<class T>
void insertion_sort(vector<T>& nums) {
	for (int i = 1; i < nums.size(); i++) {
		// 将 1 - n-1 插入
		for (int j = i; j > 0 && nums[j-1] > nums[j]; j--) {
			swap(nums[j], nums[j-1]);
		}
	}
}

template<class T>
void printVector(vector<T>& nums) {
	for (auto i : nums) cout << i << " ";
	cout << endl;
}

int main() {
	vector<int> nums = { 89,45,68,90,29,34,17 };
	insertion_sort(nums);
	printVector(nums);
	return 0;
}

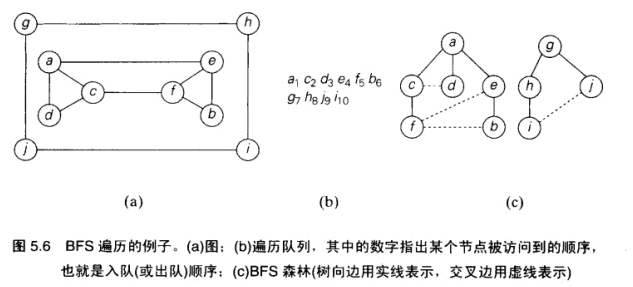
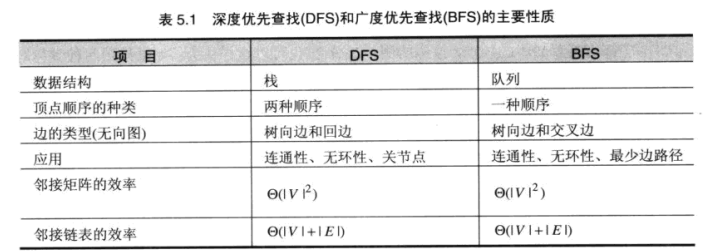
深度优先查找和广度优先查找

DFS:

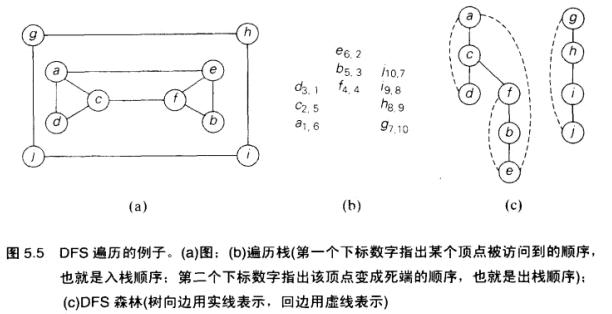
BFS:

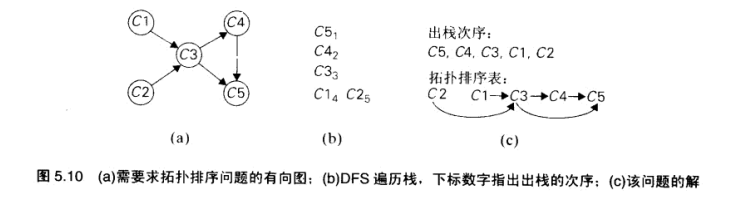
拓扑排序

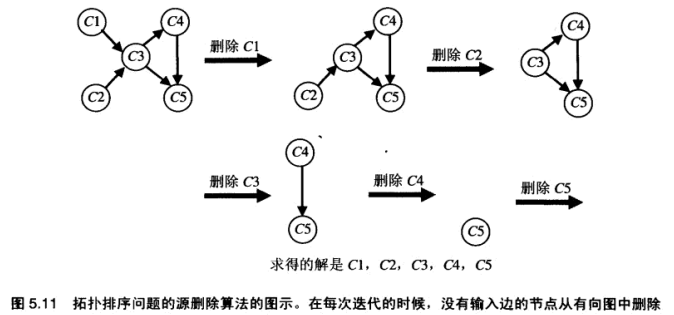
另一种方法, 源删除算法:

生成组合对象的算法

生成排列, 生成子集

减常因子算法

折半(二分)查找

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>

using namespace std;

template<class T>
int binary_search(vector<T>& nums, T target) {
	int left = 0, right = nums.size() - 1;
	while (left <= right) {
		int mid = left + (right - left) / 2;
		if (nums[mid] == target) {
			return mid;
		} else if (nums[mid] < target) {
			left = mid + 1;
		} else {
			right = mid - 1;
		}
	}
	return -1;
}


template<class T>
void printVector(vector<T>& nums) {
	for (auto i : nums) cout << i << " ";
	cout << endl;
}

int main() {
	vector<int> nums = { 89,45,68,90,29,34,17 };
	int k = binary_search(nums, 90);
	if (k != -1) {
		cout << "该数的下标为：" << k << endl;
	}
	return 0;
}

效率类型 θlog(n)

假币问题, 俄式乘法, 约瑟夫问题

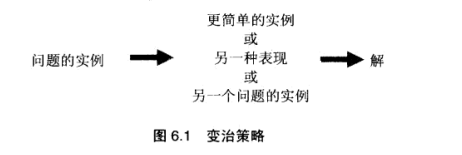
变质法

变治思想有3种主要的类型:
变换为同样问题的一个更简单或者更方便的实例——我们称之为实例化简。
变换为同样实例的不同表现——我们称之为改变表现。
变换为另一个问题的实例，这种问题的算法是已知的——我们称之为问题化简。

预排序

矩阵运算

AVL二叉查找树

堆和堆排序

霍纳法则

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include<bits/stdc++.h>
using namespace std;

template<class T>
T horner_rule(vector<T> params, T x) {
	T res = 0;
	for (int i = 0; i < params.size(); i++) {
		res = x * res + params[i];
	}
	return res;
}

int main() {
	vector<int> params = { 2, -1, 3, 1, -5 };
	cout << horner_rule(params, 3) << endl;
	return 0;
}

乘法次数和加法次数

问题化简

将不知道求解的问题化简为已知到求解问题的组合.

最小公倍数

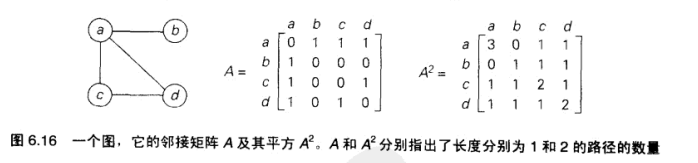
计算图中路径数量

领接矩阵幂运算

优化问题的化简, 线性规划, 简化为图

时空权衡

输入增强: 对问题的部分或全部输入做预处理，然后对获得的额外信息进行存储，以加速后面问题的求解
空间换时间, 额外空间实现更方便的数据存取, 这种放法成为预购造.

  • 计数法排序
  • Boyer-Moore字符串匹配算法和Horspool提出的简化版本

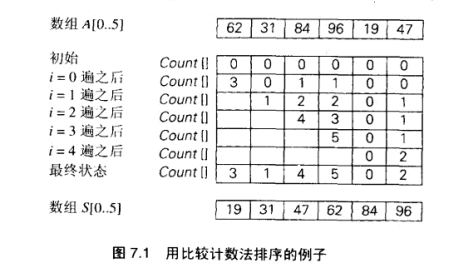
比较计数排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include<bits/stdc++.h>
using namespace std;

template<class T>
void count_sort(vector<T>& nums) {
	vector<T> rank(nums.size(), 0);
	vector<T> res(nums.size());
	for (int i = 0; i < nums.size()-1; i++) {
		for (int j = i+1; j < nums.size(); j++) {
			if (nums[i] > nums[j]) {
				rank[i]++;
			} else {
				rank[j]++;
			}
		}
	}
	for (int i = 0; i < nums.size(); i++) res[rank[i]] = nums[i];
	nums = res;
}

template<class T>
void printVector(vector<T>& nums) {
	for (auto i : nums) cout << i << " ";
	cout << endl;
}

int main() {
	vector<int> nums = { 62,31,84,96,19,47 };
	count_sort(nums);
	printVector(nums);
	return 0;
}

分布计数

同样的思想

字符串匹配中的输入增强技术

Horspool算法
Boyer-Moore算法

散列法

B树

动态规划

多阶段决策过程最优的通用方法, 特殊的空间换时间权衡.

计算二项式系数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
#include <iostream>
#include <vector>

using namespace std;

// 递归写法
int nest_binomialCoefficient(int n, int k) {
    if (k == 0 || k == n) {
        return 1;
    } else {
        return binomialCoefficient(n-1, k-1) + binomialCoefficient(n-1, k);
    }
}

// 动态规划
int binomialCoefficient(int n, int k) {
	vector<vector<int>> dp(n + 1, vector<int>(k + 1, 0));
	for (int i = 0; i <= n; i++) {
		dp[i][0] = 1;
	}
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= k; j++) {
			if (j <= i) {
				dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j];
			}
		}
	}
	return dp[n][k];
}

int main() {
	int n = 5, k = 2;
	int result = binomialCoefficient(n, k);
	cout << "C(" << n << "," << k << ") = " << result << endl;
	return 0;
}

Warshall 算法

计算有向图的传递闭包矩阵.

这个式子是建立起递推的关键, r^{k}_{ij} 取决于 r^{k-1}_{ij} 或者 r^{k-1}_{ik} 和 r^{k-1}_{kj} 的与;

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <vector>

using namespace std;

void transitiveClosure(vector<vector<int>>& graph) {
	int n = graph.size();
	vector<vector<int>> closure(n, vector<int>(n, 0));
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			closure[i][j] = graph[i][j];
		}
	}
	for (int k = 0; k < n; k++) {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				closure[i][j] = closure[i][j] || (closure[i][k] && closure[k][j]);
			}
		}
	}
	cout << "Transitive closure:" << endl;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			cout << closure[i][j] << " ";
		}
		cout << endl;
	}
}

int main() {
	vector<vector<int>> graph = {
		{0, 1, 0, 0},
		{0, 0, 1, 0},
		{1, 0, 0, 1},
		{0, 0, 0, 1}
	};
	transitiveClosure(graph);
	return 0;5
}

动态规划就是以空间换时间的技术, 将原问题分解成若干子问题, 将子问题的接缓存到数组中, 避免重复计算. 记忆化搜索, 在需要的时候利用子问题的解. 有点像虚拟机中的快照, 虚拟机将状态保存到磁盘, 以便在需要的时间恢复运用, 也是一种空间换时间, 记忆化搜索.
我查到的 Warshall 算法和Floyed算法是一个算法, 就是Warshall-Floyed算法, 书上把分为计算传递闭包和最短路径分开来了,不知道为什么. 总的思想都一样, 就是利用高阶矩阵的递推规律每次更新结果. 普遍的只要是存储更新矩阵都能使用.

Floyd 算法

计算最短路径
Warshall算法中更新的表示可达性的布尔矩阵, Floyd算法中更新的是距离矩阵, 思想都一样, 还是矩阵的幂运算的递推式, 不过计算的是最短距离, 要改下条件:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
#include <iostream>
#include <vector>
using namespace std;
#define INF INT_MAX

void floyd(vector<vector<int>>& graph) {
	int n = graph.size();
	vector<vector<int>> dist(n, vector<int>(n));
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			dist[i][j] = graph[i][j];
		}
	}
	for (int k = 0; k < n; k++) {
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if (dist[i][k] != INF && dist[k][j] != INF) {
					dist[i][j] = min(dist[i][j], dist[i][k] + dist[k][j]);
				}
			}
		}
	}
	cout << "All pairs shortest paths:" << endl;
	for (int i = 0; i < n; i++) {
		for (int j = 0; j < n; j++) {
			if (dist[i][j] == INF) {
				cout << "INF\t";
			} else {
				cout << dist[i][j] << "\t";
			}
		}
		cout << endl;
	}
}

int main() {
	vector<vector<int>> graph = {
		{0, 5, INF, 10},
		{INF, 0, 3, INF},
		{INF, INF, 0, 1},
		{INF, INF, INF, 0}
	};
	floyd(graph);
	return 0;
}

最优二叉查找树OBST

二叉查找树是最重要的数据结构之一。它的一种最主要应用是实现字典，这是一种具有查找、插入和删除操作的元素集合。在 OBST 中，我们希望将搜索代价最小，即查找任意一个元素的平均代价最小。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <vector>
#include <climits>

using namespace std;

int optimalBST(vector<float>& p, vector<float>& q, int n) {
    vector<vector<float>> w(n + 2, vector<float>(n + 1));
    vector<vector<int>> c(n + 2, vector<int>(n + 1));
    vector<vector<int>> r(n + 1, vector<int>(n + 1));
    for (int i = 1; i <= n + 1; ++i) {
        w[i][i - 1] = q[i - 1];
        c[i][i - 1] = 0;
    }
    for (int len = 1; len <= n; ++len) {
        for (int i = 1; i <= n - len + 1; ++i) {
            int j = i + len - 1;
            w[i][j] = w[i][j - 1] + p[j - 1] + q[j];
            c[i][j] = INT_MAX;
            for (int k = i; k <= j; ++k) {
                int cost = c[i][k - 1] + c[k + 1][j] + w[i][j];
                if (cost < c[i][j]) {
                    c[i][j] = cost;
                    r[i][j] = k;
                }
            }
        }
    }
    return c[1][n];
}

int main() {
    vector<float> p = {0.15, 0.1, 0.05, 0.1, 0.2};
    vector<float> q = {0.05, 0.1, 0.05, 0.05, 0.05, 0.1};
    int n = p.size();
    int cost = optimalBST(p, q, n);
    cout << "The minimum cost of OBST is " << cost << endl;
    return 0;
}

动态规划解背包问题

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
#include <iostream>
#include <vector>
using namespace std;

int knapsack(vector<int>& w, vector<int>& v, int W) {
    int n = w.size();
    vector<vector<int>> dp(n + 1, vector<int>(W + 1, 0));

    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= W; j++) {
            if (j >= w[i - 1]) {
                dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - w[i - 1]] + v[i - 1]);
            } else {
                dp[i][j] = dp[i - 1][j];
            }
        }
    }

    return dp[n][W];
}

int main() {
    vector<int> w = {2, 3, 4, 5};
    vector<int> v = {3, 4, 5, 6};
    int W = 8;
    int max_value = knapsack(w, v, W);
    cout << "The maximum value is: " << max_value << endl;
    return 0;
}

该算法的时间效率和空间效率都属于θ(nW)。用来求最优解的具体组成的时间效率属于0(n+W)。
dp[i][j] 只依赖于 dp[i-1][j] 和 dp[i-1][j-w[i]]，因此我们可以使用一维数组来表示 dp 数组，从而将空间复杂度从 O(nV) 优化到 O(V)。

贪婪技术

Prim 算法

连通图的一棵生成树是包含图的所有顶点的连通无环子图(也就是一棵树)。加权连通图的一棵最小生成树是图的一棵权重最小的生成树，其中，树的权重定义为所有边的权重总和。最小生成树问题就是求一个给定的加权连通图的最小生成树问题。

从任意一个顶点开始, 作为生成树的起点, 选取相邻的权值最小的边加入(不可形成环), 直至加入全部节点.

Kruskal 算法

同样用来构造最小生成树, Prim算法从顶点入手, Kruskal算法从边入手.
从最短边开始, 不断加入相邻的边直至|V|-1条包含所有节点, 不能形成环, 选取权值最小的边.

Dijkstra 算法

念 /ˈdɛɪkstra/
带权图中单源最短路径的贪心算法
跟Prim算法很像, 不过目标和更新操作不一样.
核心是比较当前节点直接通往下一个节点和当前节点绕过一个节点再到达下一节点谁的权值小.

Dijkstra 算法的时间复杂度为 O(V^2)，其中 V 表示节点的数量。如果使用优先队列来优化算法，可以将时间复杂度降为 O(E log V)，其中 E 表示边的数量。因此，Dijkstra 算法适用于节点数量较少，但边的数量较多的图。

哈夫曼树哈夫曼编码

算法能力的极限

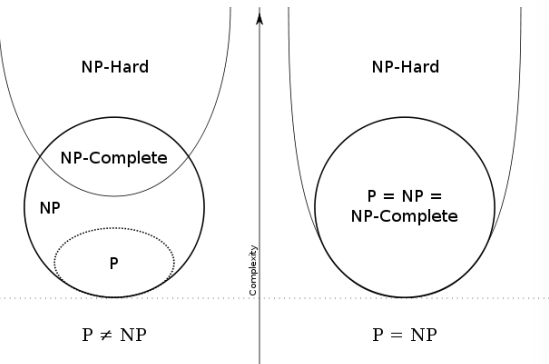
P NP 和 NP完全问题

我们把可以在多项式时间内求解的问题称为易解的，而不能在多项式时间内求解的问题则称为难解的
P类问题是一类能够用(确定性的)算法在多项式的时间内求解的判定问题。这种问题类型也称为多项式类型。

某些判定问题是不能用任何算法求解的。我们把这种问题称为是不可判定问题。

NP类问题是一类可以用不确定多项式算法求解的判定问题。我们把这种问题类型称为不确定多项式类型
P属于NP

简单来说, P 类问题是一个判定问题, 判定在在多项式时间的算法类型可不可解, 可接就是P类问题, 大多数问题都是P类, 可以通过分析得出算法的时间效率.
NP问题也是一个判定问题, 不过判定的对象是不确定算法, 即不可以通过分析直接得出效率类型, 效率类型不确定, 需要进行猜测和验证在多项式时间内能不能给出有效解.这里的N指的nondeterministic.

NPC问题 NP Complete, 即NP完全问题. 建立在NP基础之上, 属于NP问题. 如果D是NPC问题, NP中的其他问题都能在多项式的时间类化简为D. 这意味着只要能判定一个问题为NPC, 再基于NPC问题这个典型, 将P = NP ? 的终极问题化简为 P = NPC ? 的问题.

其他

  1. 一些算法特性

参考

  1. 算法设计与分析基础 第二版 清华大学出版社
  • Author:

    slacr_

  • Copyright:

  • Published:

    June 19, 2023

  • Updated:

    June 19, 2023

Buy me a cup of coffee ☕.

支
read 1000000
1 绪论&算法效率分析
1.1 算法概念
1.2 算法的特性
1.3 重要的问题类型
1.4 欧几里得算法求最大公约数GCD(Greatest Common Divisor)
1.5 基本数据结构
1.6 算法效率分析
1.7 算法最优 最差 平均效率
1.8 渐进符号
1.9 基本渐进效率类型
1.10 非递归算法效率分析一般步骤
1.11 递归算法分析
1.11.1 Fibonacci数列
2 蛮力法
2.1 选择排序和冒泡排序
2.2 顺序查找和蛮力字符串匹配
2.3 最近对问题和凸包问题暴力算法
2.4 穷举查找
3 分治法
3.1 合并排序 快速排序
3.2 二叉树遍历
3.3 大整数乘法和Srassen矩阵乘法
3.4 分治法解最近对和凸包问题
4 减治法
4.1 插入排序
4.2 深度优先查找和广度优先查找
4.3 拓扑排序
4.4 生成组合对象的算法
4.5 减常因子算法
4.5.1 折半(二分)查找
4.5.2 假币问题, 俄式乘法, 约瑟夫问题
5 变质法
5.1 预排序
5.2 矩阵运算
5.3 AVL二叉查找树
5.4 堆和堆排序
5.5 霍纳法则
5.6 问题化简
5.6.1 最小公倍数
5.6.2 计算图中路径数量
5.6.3 优化问题的化简, 线性规划, 简化为图
6 时空权衡
6.1 比较计数排序
6.2 分布计数
6.3 字符串匹配中的输入增强技术
6.4 散列法
6.5 B树
7 动态规划
7.1 计算二项式系数
7.2 Warshall 算法
7.3 Floyd 算法
7.4 最优二叉查找树OBST
7.5 动态规划解背包问题
8 贪婪技术
8.1 Prim 算法
8.2 Kruskal 算法
8.3 Dijkstra 算法
8.4 哈夫曼树哈夫曼编码
9 算法能力的极限
9.1 P NP 和 NP完全问题
10 其他